How to use Differentiation to find the gradient at a point

Before reading this post, I would strongly recommend looking at my other post of how to differentiate if you do not know how to do so already.

Assuming you know how to differentiate equations; lets begin.


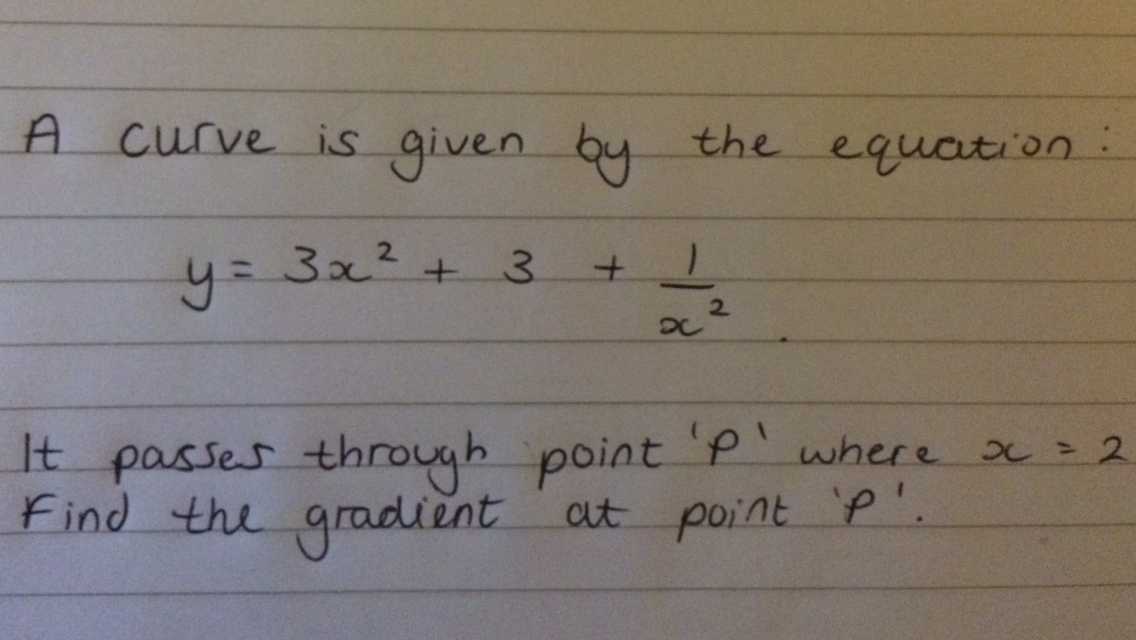
Here is an example of a common question that involves dy/dx:



First of all breaking down the question it is basically asking you to differentiate the equation, then substitute the value of x to find the gradient at point P.

This is simply done and using simple algebra and substitution we can derive that the gradient has a value of 11.




Very Easy...

We could also be asked this question:


The steps to approaching this would be to:

1) Use the gradient we have already found to find the gradient of the normal.

2) Use substitution to find the value of y

3) Use the new values to find the value of c and complete the equation.



The image below shows using -1/m to find the perpendicular gradient.

Then we use the original formulae of the curve to find the value of y, as shown here -------->










 We then substitute the values of x and y into our new equation in the form of:

y=mx + c

We then find that c = 15.48.

We now have the equation as shown :)